| 研究動機(管理人補足) 軽兵衛研究員はある日、愛車のアクティを横から見たとき、前輪と後輪で空気圧が違うので、タイヤの潰れ方がかなり違うことに気が付きました。 このまま走れば前後の回転数に差が生じ、ビスカスカップリングに負担がかかり続けるのではないか。前後重量配分が50:50に近いアクティでほとんど空荷で走るには、前後の空気圧を同一にすれば燃費が良くなるのではないかと考え、では空気圧の違いで回転数にどれだけ差があるのか。会議室で空気圧が話題になったことをきっかけに調査しました。 空気圧と積載量がタイヤ回転数に与える影響  ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ タイヤの空気圧変化や荷重変化により生じる前後輪の回転差に関する実験を行いました。現実的には「回転数」そのものを正確に測定することは困難なため、本実験では「実効外周長(タイヤが1回転して進む距離)」を実測し、その逆数から「回転数」を計算しました。 《おことわり》 本実験結果は限られた条件下で得られたものですので、他の条件では結果も異なります。また、車種やタイヤが異なる場合はもちろん、実験に使用したものと同じタイヤを使用しても、摩耗状態等により微妙な差が生じます。なお測定誤差や計算ミスもあろうかと思いますので、結果はあくまでも「参考程度」とご理解ください。 ★ お急ぎの方は最後の《まとめ》へどうぞ ★ 【実験1】空気圧とタイヤ実効外周長の関係  ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ 《条 件》 実験車:HONDA ACTY HA7 SDX 5MT (前輪のみビスカスカップリングで制御する方式のリアルタイム4WD) タイヤ:BS "B-Style"(155/70R13)←走行6000kmの八分山 ホイール:13×4.5J アルミ 測定タイヤ:右後輪 積載:なし 乗員:走行実験時は一名(50kg)乗車 静止実験時は運転席に50kgのダミーウェイトを積載 《測定項目》 空気圧を「325kPa(+30%)→250kPa(基準)→175kPa(-30%)」と変化させ、下記の3項目について実測しました。 〔A〕ハブ中心高さ(以下「荷重半径」と呼びます) 曲尺を使用して路面からハブ中心までの高さを測定しました。 〔B〕タイヤ接地長 タイヤ接地部分の長さです。タイヤ外周部が「円弧」でなく「弦」となる部分で、接地部の前後に差し込んだ二枚のハガキの間隔を測定しました。 〔C〕タイヤが120回転して進む距離 絶対的な距離ではなく、まず地図から約200mと推定される直線路にて、印を付けたタイヤ(空気圧250kPa)が120回転して進む距離を便宜上「200m」と定めて路面にマーク。次に空気圧を変更して、タイヤが120回転して進んだ位置と路面マークとの間隔を相対的に測定しました。250kPa時の走行距離を基準(100%)として「相対的実効外周長(1回転で進む相対距離)」を計算します。 《実測データ》 [実測値] ───────────────── 空気圧 荷重半径 接地長 120回転 の距離 (kPa) (mm) (mm) (m) ───────────────── 325 261.2 98 200.5 250 259.0 107 200.0 ←基準値 175 254.7 125 199.58 ───────────────── [250kPa時を基準とした相対値] ─────────────────────── 空気圧 荷重半径 接地長 実効外周長 ─────────────────────── +30%(325kPa) +0.85% -8.41% +0.25% 0%(250kPa) 0% 0% 0% -30%(175kPa) -1.66% +16.82% -0.21% ─────────────────────── 【実験2】積載量とタイヤ実効外周長の関係  ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ 《条 件》 実験車およびタイヤ:【実験1】に同じ 空気圧:四輪とも250kPa 測定タイヤ:右後輪 乗員:走行実験時は一名(60kg)乗車 静止実験時は運転席に50kgのダミーウェイトを積載 《実験項目》 荷台中央部に質量100kg、200kgおよび300kgの荷物を段階的に積載して以下の項目を実測しました。 ※質量100kgを荷台中央部に積載した場合、後車軸には84.3kgが配分されます。「荷重」の正式なSI単位「N(ニュートン)」を使用すると、後車軸にかかる荷重は「826N」となりますが、ここでは慣用単位である「kg」で代用しました。また、燃料の質量は計算に入れてありません。 〔D〕ハブ中心高さ(荷重半径) 【実験1】に同じ 〔E〕タイヤ接地長 【実験1】に同じ 〔F〕タイヤが120回転して進む距離 【実験1】に同じ。ただし空気圧は250kPa一定で積載量のみを変化。 《実測データ》 [実測値] ──────────────── 積載量 荷重 接地長 120回転 半径 の距離 (kg) (mm) (mm) (m) ──────────────── 0 259.0 113 200.00 ←これを基準とする 100 257.0 121 199.88 200 254.5 127 199.78 300 252.5 137 199.69 ──────────────── ※ジャッキアップ時のタイヤ実測半径は273mm(基準値259mmの+5.4%) [無積載時を基準としたときの相対値] ─────────────────────────────────── 積載量 後軸荷重 荷重半径 接地長 実効外周長 前軸配分 後軸配分 ─────────────────────────────────── 0kg +0% +0% +0% +0% 52.4% 47.6% 100kg +19.67% -0.77% +7.08% -0.060% 48.7% 51.3% 200kg +39.34% -1.74% +12.39% -0.110% 45.7% 54.3% 300kg +59.01% -2.51% +21.24% -0.155% 43.2% 56.8% ─────────────────────────────────── ※基準となる無積載後軸荷重は428.6kg 【実験3】荷重状態と空気圧の関係  ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ 空荷状態にて空気圧を250kPaに設定した右後輪をジャッキアップして空気圧変化を測定しましたが、ゲージで読み取れるほどの差は生じませんでした。 《実験結果》 【1.空気圧変化実験より】 〔1〕空気圧を250kPaから325kPaに30%加圧した場合の荷重半径変化はプラス2.2mm(0.85%)でしたが、逆に250kPaから175kPaに30%減圧した場合にはマイナス4.3mm(1.66%)でした。従って、空気圧変化と荷重半径変化との間に直線的な比例関係はなく、空気圧が低いほど荷重半径に与える影響は大きくなります。⇒〔グラフ 1〕 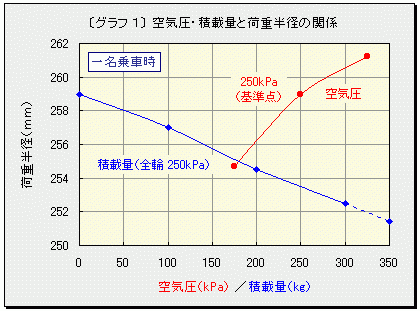 〔2〕空気圧が250kPaから325kPaに増加した場合、荷重半径2.2mmの変化に対して実効外周長変化は0.25%ですが、逆に250kPaから175kPaに減少する方向では、4.3mmの変化に対して同0.21%と係数は半減しました。従って同じ荷重半径変化量であっても、空気圧を低くするより高くする方が、実効外周長(言い換えれば回転数)に与える影響は大きくなります。⇒〔グラフ 2〕 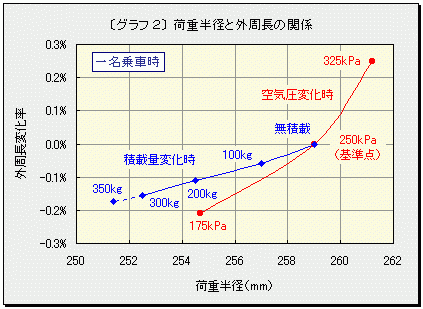 半径を「r」とした場合、鉄道車輪のような剛体車輪の外周長は単純に「2πr」となりますが、柔軟なタイヤの場合には、荷重半径を「r」として計算しても、実効外周長は「2πr」とはなりません。これは後述の「スチールベルト=タガ理論」からご理解戴けると思います。 〔3〕標準空気圧を250kPaとした場合、空気圧を±30%変化させた場合の実効外周長変化はプラス側0.25%/マイナス側0.21%で、タイヤの空気圧と実効外周長との間にはほぼ比例関係が見られます(タイヤ回転数とは反比例)。これを空気圧変化±10%あたりに換算すると、実効外周長変化率はプラス側で0.083%、マイナス側で0.07%となります。現実的には、空気圧を1割上げればスピードメーターは0.083%アンダーに出るし、1km走行した場合には同じタイヤ回転数で走行距離が83cm長くなることを意味します。⇒〔グラフ 3〕 ※便宜上「ほぼ比例」と表現しましたが、後述のシミュレーションでは実データにフィットさせた2次曲線で近似しました。 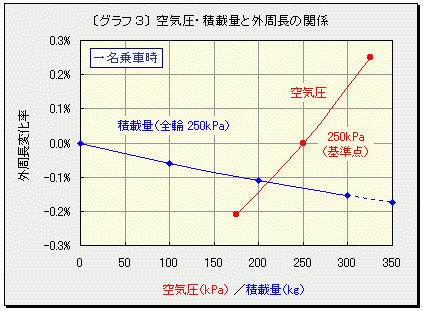 通常のラジアルタイヤは、スチールベルトという「タガ」で外周をがっちり締め付けられているので、極端に空気圧が低下してタイヤが大幅に変形しない限り、空気圧がタイヤ実効外周長に与える影響は軽微なものです。これは私が「スチールベルト=タガ理論」と名付けているもので、「紙テープで作ったリングの一部を机に押し付けて転がす(=クローラー的動作)」というイメージでご理解戴けると思います。 タイヤの断面形状は使用目的や扁平率により異なります。例えば扁平率50%以下のスポーツタイヤではトレッド部断面がフラットに近いし、扁平率の高い実用タイヤでは丸みを帯びてきます。丸みを帯びた結果、ショルダー部と中央部とでは外周長に僅かな差が生じます。空気圧が「低→適正→高」と変化すると、タイヤの主な接地部は「ショルダー部→全体→中央部」へと移動します。その結果、空気圧が増加すると僅かながらも外周長が増加し、1回転で進む距離も長くなります。この現象はトレッド部断面の曲率が大きくなるほど顕著に現れますので、ショルダー部が偏摩耗した自動車タイヤや、自転車・バイク用タイヤのように断面が円形のタイプでは、より空気圧変化の影響を受け易いものと推測します。 〔4〕「タイヤ接地長」つまり荷重によりタイヤが変形して「弦」となる部分の長さと実効外周長には直接の関係はありませんでした。 空気圧を250kPaから325kPaに増加した時の「弧−弦の差」は円周長の0.0095%なのですが、実効外周長差は26倍の0.25%となります。一方、250kPaから175kPaに減少した場合、円周長に対する「弧−弦の差」は0.025%ですが、実際には8.4倍の0.21%です。荷重によりタイヤが変形して「弦」となった部分が「弧」より短くなることは明らかですが、その差は分散されてスチールベルトの長さ自体の変化は生じないことになります。 【2.積載量変化実験より】 〔5〕空気圧を四輪とも250kPaに設定し、積載量を0kg、100kg、200kg、300kgと変化した実験からは、以下の関係が見られました。 ※プロットしたグラフが多少曲線的であっても、ここでは便宜上「比例」もしくは「反比例」と表現しました。ただし、後述のシミュレーションには実データにフィットさせた3次曲線を使用しました。 ●「積載量と荷重半径」は反比例。⇒〔グラフ 1〕 ●「荷重半径と実効外周長」は比例(回転数とは反比例)。⇒〔グラフ 2〕 ● 従って「積載量と実効外周長」は反比例(回転数とは比例)。⇒〔グラフ 3〕 ● 荷台中央(または平均的)に100kgを積載するごとに実効外周長は約0.06%短縮する(約0.06%回転数が増加する)。同様に350kg積載時には実効外周長が0.17%ほど短縮する。⇒〔グラフ 3〕 ● 同じ荷重半径変化量であっても、積載量変化よりも空気圧変化の方が実効外周長(もしくは回転数)に与える影響は大きい。例えば荷重半径が259mmから4.5mmほど減少した場合、積載量が0kgから200kgに増加するより空気圧が250kPaから175kPaに減少する方が実効外周長に与える影響は2倍となる。⇒〔グラフ 2〕 参考のため「積載量と前後軸荷重配分および荷重半径との関係」を〔グラフ 4〕に示します。積載量62.3kgの時に前後軸荷重配分が等しくなることがわかります。 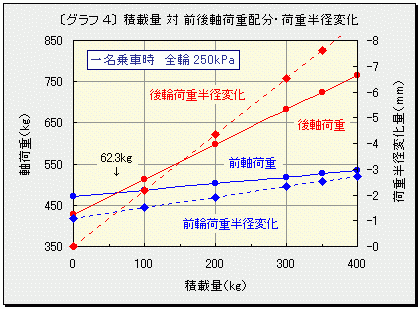 【ジャッキアップ前後の空気圧変化実験より】 〔6〕タイヤ1本あたり205kg程度(2.01kN)の荷重変化は空気圧に対してほとんど影響を与えません。 ちょっと意外な結果となりましたが、考えてみればタイヤにはカーカスコードやスチールベルトという「骨格」があるため、ゴム風船のように伸び縮みはしません。そのため通常範囲内では、荷重により変形はしても体積には大きな変化が生じないため「ボイル・シャルルの法則」から、充填された空気の「分子量、体積、温度が変化しない限り圧力は一定」となります。 《アクティHA7の場合のシミュレーション》 実験結果を基に近似式を求め、一名(体重60kg)乗車の条件にて、空気圧と積載量を変化した時の前後輪回転差をEXCEL上でミュレーションしてみました。なお「前220kPa/後300kPa」の曲線は参考として入れました。⇒〔グラフ 5〕 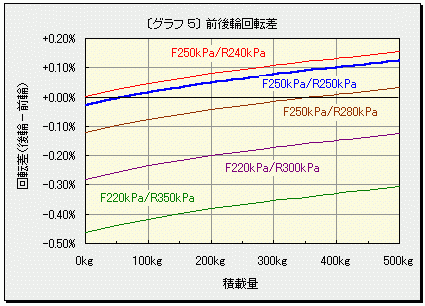 〔前:250kPa/後:250kPa 無積載〕←私の常用空気圧 荷重配分は前:471.4kg/後:428.6kg。後輪回転数は前輪に対し-0.03%。 前:250kPa/後:240kPaにすると前後輪回転数はバランス。 また、前:250kPa/後:250kPaでも、荷台中央(または均等)に62.3kgの荷物を積載した場合、車体重心はホイールベース中央となり、前後輪回転数はバランス。 〔前:250kPa/後:250kPa 350kg積載〕 荷重配分は前:526.4kg/後:723.6kg。後輪回転数は前輪に対し+0.09%。 前:250kPa/後:280kPaにすると前後輪回転数はバランス。 〔前:220kPa/後:350kPa 無積載〕←メーカー指定空気圧 荷重配分は前:471.4kg/後:428.6kg。後輪回転数は前輪に対し-0.46%。 〔前:220kPa/後:350kPa 350kg積載〕 荷重配分は前:526.4kg/後:723.6kg。後輪回転数は前輪に対し-0.34%。 250kPa以外でのシミュレーションは250kPa時の実測データを使用したものですので、実際とは多少異なるかもしれません。メーカー指定の空気圧設定では、無積載時に0.46%もの前後輪回転差が生じますが、その程度はビスカスカップリングが吸収し、タイトコーナーブレーキング的効果はほとんど問題とはならないのかも知れません。 《まとめ》 最後に、アクティの場合に限られますが、要点だけをまとめます。 ■ 空気圧1割の変化に対し、タイヤ回転数は0.08%程度の係数で反比例。 ■ 荷重によりタイヤ荷重半径が1%(2.7mm)変化した場合の回転数に与える影響は0.06%程度。 ■ 空気圧250kPaにて、積載量100kgごとに後輪回転数は約0.06%増加。 ■ 荷重半径の変化量が同じであっても、積載量による変化より空気圧による変化の方が、タイヤ回転数に与える影響は2倍。 ■ 一名乗車・無積載の場合、後輪側-10kPaで前後回転数はバランス。 また、一名乗車・350kg積載時では、後輪側+30kPaで前後輪回転数はバランス。 結論として、特に空荷か軽量積載の条件では、操縦特性(アンダー/オーバーステア)、接地性(コーナリング/ブレーキング)、乗り心地、偏摩耗、路面状況(ターマック/グラベル/ドライ/ウエット)等を総合的に考慮すると、後輪をメーカー指定の350kPaまで上げなくても良いように思います。実際、私の場合は四輪とも250kPaに設定していますが、特に不都合を感じたことはありません。 ※ただし、0.01%から0.1%の精度で前後輪の回転差を検出して各種のコントロールをしている場合には、この限りではないことを申し添えます。 (管理人補足) ほとんどの軽トラックには空荷時と積載時の空気圧が表示されています。空気圧を高くすると走りが軽快になって燃費も良くなりますが、グリップが弱くなり、いざという時に止まらなかったり、乗り心地が悪くなります。そこで普通は空荷と積載時で空気圧を変えるように指定されています。通常空荷時には前後輪共200kPa台に設定されている車が多いです。 積載時の後輪空気圧は、最近は145R12-6PRの規定めいっぱいの350kPaに指定する車が多くなりました。 新規格アクティの場合は、積載時の空気圧しか指定されていません。後輪が8PR(初期型)/6PR(後期型)規定めいっぱいの450kPa/350kPaです。それを信じてめいっぱい詰めると、乗り心地は悪いやら、ブレーキはきかないやら、ABS装着車はほんのちょっとしたことでABSがききまくり、雨の日にはヒヤっとしたことも一度や二度ではありません。果たしてこんな空気圧指定が正しいのでしょうか? ちなみに、純正が8PRの車で6PRタイヤに変更しても、ほとんどの車検場では通してくれますが、6PRの規定めいっぱいは350kPaです。 乗用車タイヤに変更した場合、実質300kPaが上限です。入れすぎないようにしてください。 アクティのMT車のカタログでは前後輪のギア比が違うことになっています。これは前後で回転数を変えて制御するものではなく、実際は他のビスカスカップリング式4WD車同様、前後同回転になっているようです。 アクティはリヤデフの先にカウンターギヤを取り付け、更にベベルギヤで90度回転させ、ビスカスカップリングを介して介して前輪に伝える仕組みになっています。この取り出し部分のギア比が明記されていないため、誤解が生ずるようです。 エンジン縦置きの4WD・4AT車の前後ギア比が同一であること、空気圧指定の違うトラック、バン、バモスのこの部品が同じ物であることから、回転数の差をギア比で補うというようなものではなく、同回転であることが推測されます。 センターデフやカップリングなどの装置をもたないパートタイム4WD車の場合は、僅かな差を吸収できないことになります。実際には内輪差による誤差の方が遥かに大きく、どっちみちグリップのあるアスファルト路では4WDでは長く走れません。問題になることはないでしょう。 <謎>なぜアクティは空荷時の時の空気圧が指定されていないのか? この件に関してはHondaの方とお話する機会があれば調査したいと思います。 サイトとしての建て前上、指定空気圧以外に変更することは自己責任でということでお願いします。 |